Face Recognition/Authentication Using Support Vector Machines

This post is part of a series on face recognition, I have been posting on face recognition for a while. There would be at least 7-8 more posts in the near future on the topic. Though I can not promise a time frame within which all would be up.

Previous Related Posts:

1. Face Recognition using Eigenfaces and Distance Classifiers – A Tutorial

2. Face Recognition in Bees

3. A Huge Collection of Datasets (Post links to a number of face image databases)

4. Why are Support Vector Machines called so?

This post would reference two of my posts. One on SVMs and the other on Face Recognition using Eigenfaces.

Note: This post focuses on the idea behind using SVMs for face recognition and authentication. In future posts I will cover the various packages that can be used to implement SVMs and how to go about using them, and specifically for face recognition. The same can be easily extended to other similar problems such as content based retrieval systems, speech recognition, character or signature verification systems as well.

_____

Difference between Face Authentication (Verification) and Face Recognition (also called identification):

This might seem like a silly thing to start with. But for the sake of completeness, It is a good point to start with.

Face Authentication can be considered a subset of face recognition. Though due to the small difference there are a few non-concurrent parts in both the systems.

Face Authentication (also called verification) involves a one to one check that compares an input image (also called a query image, probe image or simply probe) with only the image (or class) that the user claims to be. In simple words, if you stand in front of a face authentication system and claim to be a certain user, the system will ONLY check if you are that user or not.

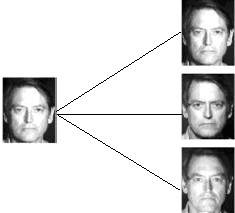
Face Recognition (or Identification) is another thing, though ofcourse related. It involves a one to many comparison of the input image (or probe or query image) with a template library. In simple words, in a face recognition system the input image will be compared with ALL the classes and then a decision will be made so as to identify to WHO the the input image belongs to. Or if it does not belong to the database at all.

Like I just said before, though both Authentication and Recognition are related there are some differences in the method involved, which are obvious due to the different nature of both.

_____

A Touch-Up of Support Vector Machines:

A few posts ago I wrote a post on why Support Vector Machines had this rather “seemingly” un-intuitive name. It had a brief introduction to SVMs as well. For those completely new to Support Vector Machines this post should help. I’ll still add a little for this post.

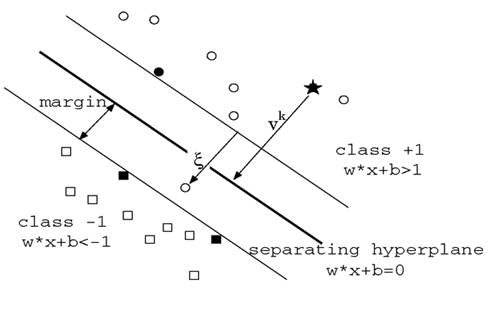
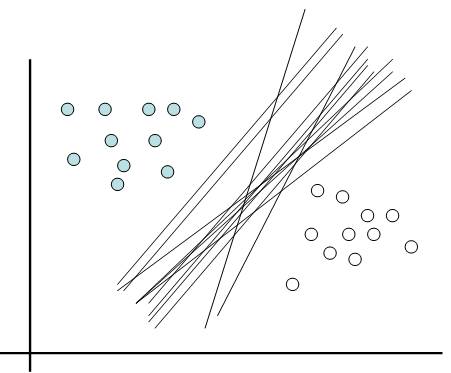
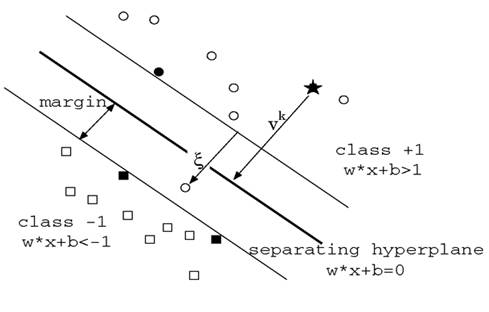
Support Vector Machine is a binary classification method that finds the optimal linear decision surface between two classes. The decision surface is nothing but a weighted combination of the support vectors. In other words, the support vectors decide the nature of the boundary between the two classes. Take a look at the image below:

The SVM takes in labeled training examples , where represents the features and the class label, that could be either 1 or -1.  On training we obtain a set of Support Vectors , multipliers , and the term . To understand what does, look at the above figure. It is somewhat like the intercept term in the equation of a straight line, . The terms and determine the orientation of the hyperplane while determines the actual position of the hyperplane.

As is indicated in the diagram, the linear decision surface is :

where

where are the support vectors.

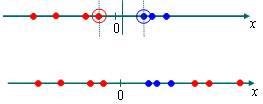
The above holds when the data (classes) is linearly separable. Sometimes however, that’s not the case. Take the following example:

The two classes are indicated by the two different colors. The data is clearly not LINEARLY separable.

However when mapped onto two dimensions, a linear decision surface between them can be made with ease.

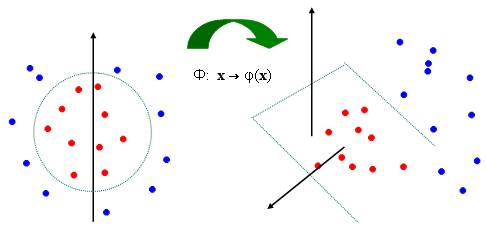
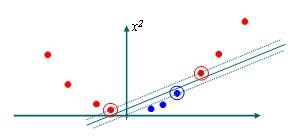Take another example. In this example the data is not linearly separable in 2-D, so they are mapped onto three dimensions where a linear decision surface between the classes can be made.

By Cover’s Theorem it is more likely that a data-set not linearly separable in some dimension would be linearly separable  in a higher dimension. The above two examples are simple, sometimes the data might be linearly separable at very high dimensions, maybe at infinite dimensions.

But how do we realize it? This done by employing the beautiful Kernel Trick. In place of the inner products we use a suitable Mercer Kernel. I don’t believe it is a good idea to discuss kernels here, or it will be a needless digression from face recognition. I promise to discuss it some time later.

Thus the non-linear decision surface changes from to:

Where represents a Kernel. It could be a Radial Basis (Gaussian) Kernel, A linear Kernel, A polynomial Kernel or a custom Kernel. :)

_____

Face Authentication is a two class problem. As I have mentioned earlier, here the system is presented with a claimed identity and it has to make a decision whether the claimant is really that person or not. The SVM in such applications will have to be fed with the images of one person, which will constitute one class and the other class will consist of images of other people other than that person. The SVM will then generate a linear decision surface.

For a input/probe image , the identity is accepted if:

Or it is rejected. We can parameterize the decision surface by modifying the above as:

Then, a claim will be accepted if for a probe,

_____

Now face recognition is a class problem. Where is the number of classes (or individuals).  Whereas the traditional Support Vector Machine is a binary classifier. So we’ll make a few changes to the way we are representing the faces to suit our classifier. I will come back to this in a while.

Feature Extraction: The faces will have to be represented by some appropriate features, these could be weights obtained using the Eigenfaces method, or using gabor features or anything else. I have written a post earlier that talked of a face recognition system based on Eigenfaces. I would direct the reader to check face representation using Eigenfaces there.

Using Eigenfaces, each probe could be represented as a vector of weights:

After obtaining such a weight vector for the input or probe image and for all the other images stored in the library, we were simply finding the Euclidean or the Mahalanobis distance of the weight vector of the probe image with those of the images in the template library.  And then were recognizing the probe as a face that gave the minimum score provided it was below a certain threshold. I have discussed this is much detail there. And since I have, I would not discuss this again here.

_____

Representation in Difference Space:

SVMs are binary classifiers, that is – they give the class which might be 1 or -1, so we would have to modify the representation of faces a little bit than what we were doing in that previous post to make it somewhat more desirable. In the previous approach that is “a view based or face space approach”, each image was encoded separately. Here, we would change the representation and encode faces into a difference space. The difference space takes into account the dissimilarities between faces.

In the difference space there can be two different classes.

1. The class that encodes the dissimilarities between different images of the same person,

2. The other class encodes the dissimilarities between images of other people. These two classes are then given to a SVM which then generates a decision surface.

As  I wrote earlier, Face recognition traditionally can be thought of as a class problem and face authentication can be thought of as a instances two class problem. To reduce it to a two class problem we formulate the problem into a difference space as I have already mentioned.

Now consider a training set having training images belonging to individuals. Each individual can have more than one image, that means ofcourse. It is from that we generate the two classes I mentioned above.

1. The within class differences set. This set takes into account the differences in the images of the same class or individual. In more formal terms:

Where and are images and indicates that they belong to the same person.

This set contains the differences not just for one individual but for all individuals.

2. The between class differences set. This set gives the dissimilarities of different images of different individually. In more formal terms:

Where and are images and indicates that they do not belong to the same person.

_____

Face Authentication:

For Authentication the incoming probe and a claimed identity is presented.

Using this, we first find out the similarity score:

We then accept this claim if it lies below a certain threshold or else reject it. I have discussed the need for a threshold at the end of this post, please have a look. is to be found heuristically.

_____

Face Recognition:

Consider a set of images , and a probe which is to be indentified.

We take and score it with every image in the set :

The image with the lowest score but below a threshold is recognized. I have written at the end of this post explaining why this threshold is important. This threshold is mostly chose heuristically.

_____

References and Important Papers

1. Face Recognition Using Eigenfaces, Matthew A. Turk and Alex P. Pentland, MIT Vision and Modeling Lab, CVPR ‘91.

2. Eigenfaces Versus Fischerfaces : Recognition using Class Specific Linear Projection, Belhumeur, Hespanha, Kreigman, PAMI ‘97.

3. Eigenfaces for Recognition, Matthew A. Turk and Alex P. Pentland, Journal of Cognitive Neuroscience ‘91.

4. Support Vector Machines Applied to Face Recognition, P. J. Phillips, Neural Information Processing Systems ’99.

5. The Nature of Statistical Learning Theory (Book), Vladimir Vapnik, Springer ’99.

6. A Tutorial on Support Vector Machines for Pattern Recognition, Christopher J. C. Burges, Data Mining and Knowledge Discovery, ’99

_____

Onionesque Reality Home >>

Read Full Post »

Why are Support Vectors Machines called so?

I am often asked by some interested friends : What ARE actually support vector machines? What kind of machines? It is obvious that such questions are put up by people who are not initiated to the idea of SVMs or even learning machines so to say.

But I have also noticed that a lot of people working in the ML/AI/Pattern Recognition domain don’t have a clear idea of why Support Vector Machines are called so. Understanding why Artificial Neural Networks are named so is not so difficult, but Support Vector Machines does sound somewhat abstruse. This is exactly what this post aims to address.

I’d be giving a short introduction first. For those who simply wish to get to the point, I would recommend them to skip to this point.

Let’s parse SVM into the three constituent words and attack them one by one – Support Vector Machines. Let’s look at Machines first.

_____

Learning Machines: Clearly this part is meant for the former category in the two I mentioned in the above introductory paragraph i.e for the uninitiated.

Let me start with a basic definition that I think is necessary to be put for the sake of mere completeness. I hope this does not disgust the more expert reader. ;-)

Machine Learning

Way back in 1959, Arthur Samuel defined Machine Learning as the field of study that gave computers the ability to learn without being explicitly programmed. Samuel was a pioneer in the area as he is widely credited to have made the first self-learning program that played checkers.

Tom Mitchell in Machine Learning puts the definition more formally as: A learning program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

Given a training set, we feed it into a learning algorithm (like SVM, Artificial Neural Nets, Logistic Regression, Linear Regression etc). The learning algorithm then outputs a function, which for historical reasons is called the hypothesis and denoted by .

So, basically the hypothesis’ job is to take a new input and give out a estimated output or class. The parameters that define the hypothesis are what are “learned” by using the training set. So the term learning machine is used in this sense.

To sum up: The hypothesis can be thought of as a machine that gives a prediction y on some unseen input x. The parameters of the hypothesis are learned (for a toy example see the part on pigeons in this post).

Ofcourse the above is defined in a supervised context but can be easily generalized.

_____

Support Vector Machines

An Introduction: I would prefer to give an extremely short introduction to SVMs first before coming to the origin of the term “Support Vectors”.

Consider the image below. How would you classify this data?

This set looks linearly separable. That means we could draw a straight line to separate the two classes (indicated by the two different colors). Also note that these data points lie in a two dimensional space, so we talk of a straight line. We could easily graduate to higher dimensions, as an example in a 3-D space we would have spoken of constructing a plane to separate the points and a hyperplane in a dimensional space.

Coming back, though we can draw a straight line to separate these two classes, there is a problem. There are an infinite number of candidate lines. Which straight line to choose?

There are two intuitions that lead us to the best hyperplane :

1. Confidence in making the correct prediction: Without getting into much detail (as the point of this post is to see why are support vector machines called so and not what they are), this intuition is formalized by the functional margin. The functional margin of a hyperplane given by w.r.t a specific training example is defined as:

If , for a large functional margin (greater confidence in correct prediction) we want

If , for a large functional margin we want .

The above captures our first intuition into a single formal statement that we would like the functional margin to be large.

2. Margin: Another intuition about choosing the best hyperplane is to choose one in which the distance from the training points is the maximum. This is formalized by the geometric margin. Without getting into the details of the derivation, the geometric margin is given by:

Which is simply the functional margin normalized. So these intuitions leads to the maximum margin classifier which is a precursor to the SVM.

To sum up: To realize these intuitions and get the best hyperplane, the optimization problem is:

Choose , , so as to maximize the geometric margin

subject to the condition that and .

Working on the above optimization problem and trying to formulate it as a convex optimization problem leads to Support Vector Machines.

Also, the data I considered was linearly separable. We could easily extend the idea to non-separable data. For the general case, the dual of the support vector machines (for non-separable data) is given as:

subject to:

,

The solution is given by:

where is the number of support vectors and the s represent the Lagrangian multipliers.

[I have not made the above diagram by myself. I had taken it quite a while back and don’t remember from where. In case you do know, please do point out]

Support Vectors?

Now that a brief introduction is done, let’s come back to the main point.

In the above diagram we see that the thinner lines mark the distance from the classifier to the closest data points called the support vectors (darkened data points). The distance between the two thin lines is called the margin. The Support Vectors constrain the width of the margin. And since they are very less as compared to the total number of data points, they hand us many advantages but let us not get into that.

The question is, why are these points called Support Vectors at all? To understand  this, consider a mechanical analogy. Consider that the data is in and suppose the support vector exerts a force of on a stiff sheet lying along the decision surface. represents the unit vector in the direction .

The solution then satisfies the conditions for mechanical equilibrium:

are the support vectors and denotes the vector product.

This mechanical analogy emphasizes two important points:

1. The most important data points are the support vectors as they have the maximum values of . These points exert the maximum force on the decision sheet. This force exerted is constrained to be below C for any point in the non-separable case.

2. Since the torque exerted by the support vectors comes out to be zero, we can say that these specific data points are “supporting” the hyperplane into “equilibrium”.

I think this explains how the term “Support Vectors” originates.

_____

Onionesque Reality Home >>

Read Full Post »

Demystifying Support Vector Machines for Beginners: A Reading List

Though I have worked on pattern recognition in the past I have always wanted to work with Neural Networks for the same. However for some reason or the other I could never do so, I could not even take it as an elective subject due to some constraints. Over the last two years or so I have been promising myself and ordering myself to stick to a schedule and study ANNs properly, however due to a combination of procrastination, over-work and bad planning I have never been able to do anything with them.

However I have now got the opportunity to work with Support Vector Machines and over the past some time I have been reading extensively on the same and have been trying to get playing with them. Now that the actual implementation and work is set to start I am pretty excited to work with them. It is nice that I get to work with SVMs though I could not with ANNs.

Support Vector Machine is a classifier derived from statistical learning theory by Vladimir Vapnik and his co-workers. The foundations for the same were laid by him as late as the 1970s SVM shot to prominence when using pixel maps as input it gave an accuracy comparable with sophisticated Neural Networks with elaborate features in a handwriting recognition task.

Traditionally Neural Networks based approaches have suffered some serious drawbacks, especially with generalization, producing models that can overfit the data. SVMs embodies the structural risk minimization principle that is shown superior to the empirical risk minimization that neural networks use. This difference gives SVMs the greater ability to generalize.

However learning how to work with SVMs can be challenging and somewhat intimidating at first. When i started reading on the topic I took the books by Vapnik on the subject but could not make much head or tail. I could only attain a certain degree of understanding, nothing more. To specialize in something I do well when I start off as a generalist, having a good and quite correct idea of what is exactly going on. Knowing in general what is to be done and what is what, after this initial know-how makes me comfortable I reach the stage of starting with the mathematics which gives profound understanding as anything without mathematics is meaningless. However most books that I came across missed the first point for me, and it was very difficult to make a headstart. There was a book which I could read in two days that helped me get that general picture quite well. I would highly recommend it for most who are in the process of starting with SVMs.The book is titled Support Vector Machines and other Kernel Based Learning methods and is authored by Nello Cristianini and John-Shawe Taylor.

I would highly recommend people who are starting with Support Vector Machines to buy this book. It can  be obtained easily over Amazon.

This book has very less of a Mathematical treatment but it makes clear the ideas involved and this introduces a person studying from it to think more clearly before he/she can refine his/her understanding by reading something heavier mathematically. Another that I would highly recommend is the book Support Vector Machines for Pattern Classification by Shigeo Abe.

Another book that I highly recommend is Learning with Kernels by Bernhard Scholkopf and Alexander Smola. Perfect book for beginners.

Only after one has covered the required stuff from here that I would suggest Vapnik’s books which then would work wonderfully well.

Other than the books there are a number of Video Lectures and tutorials on the Internet that can work as well!

Below is a listing of a large number of good tutorials on the topic. I don’t intend to flood a person interested in starting with too much information, where ever possible i have described what the document carries so that one could decide what should suffice for him/her on the basis of need. Also I have star-marked some of the posts. This marks the ones that i have seen and studied from personally and found them most helpful and i am sure they would work the same way with both beginners and people with reasonable experience alike.

—

Webcasts/ Video Lectures on Learning Theory, Support Vector Machines and related ideas:

EDIT: For those interested. I had posted about a course on Machine Learning that has been provided by Stanford university. It too is suited for an introduction to Support Vector Machines. Please find the post here. Also this comment might be helpful, suggestions to it according to your learning journey are also welcome.

1. *Machine Learning Workshop, University of California at Berkeley. This series covers most of the basics required. Beginners can skip the sessions on Bayesian models and Manifold Learning.

Workshop Outline:

Session 1: Classification.

Session 2: Regression.

Session 3: Feature Selection

Session 4: Diagnostics

Session 5: Clustering

Session 6: Graphical Models

Session 7: Linear Dimensionality Reduction

Session 8: Manifold Learning and Visualization

Session 9: Structured Classification

Session 10: Reinforcement Learning

Session 11: Non-Parametric Bayesian Models

2. Washington University. Beginners might be interested on the sole talk on the topic of Supervised Learning for Computer Vision Applications or maybe in the talk on Dimensionality Reduction.

3. Reinforcement Learning, Universitat Freiburg.

4. Deep Learning Workshop. Good talks, But I’d say these are meant for only the highly interested.

5. *Introduction to Learning Theory, Olivier Bousquet.

This tutorial focuses on the “larger picture” than on mathematical proofs, it is not restricted to statistical learning theory however. The course comprises of five lectures and is quite good to watch. The Frenchman is both smart and fun!

6. *Statistical Learning Theory, Olivier Bousquet. This course gives a detailed introduction to Learning Theory with a focus on the Classification problem.

Course Outline:

Probabilistic and Concentration inequalities, Union Bounds, Chaining, Measuring the size of a function class, Vapnik Chervonenkis Dimension, Shattering Dimensions and Rademacher averages, Classification with real valued functions.

7. *Statistical Learning Theory, Olivier Bousquet. This is not the repeat of the above course. This one is a more recent lecture series than the above actually. This course has six lectures. Another excellent set.

Course Outline:

Learning Theory: Foundations and Goals

Learning Bounds: Ingredients and Results

Implications: What to conclude from bounds

7. Advanced Statistical Learning Theory, Olivier Bousquet. This set of lectures compliment the above courses on statistical learning theory and give a more detailed exposition of the current advancements in the same.This course has three lectures.

Course Outline:

PAC Bayesian bounds: a simple derivation, comparison with Rademacher averages, Local Rademacher complexity with classification loss, Talagrand’s inequality. Tsybakov noise conditions, Properties of loss functions for classification (influence on approximation and estimation, relationship with noise conditions), Applications to SVM – Estimation and approximation properties, role of eigenvalues of the Gram matrix.

8. *Statistical Learning Theory, John-Shawe Taylor, University of London. One plus point of this course is that is has some good English. Don’t miss this lecture as it has been given by the same professor whose book we just discussed.

9. *Learning with Kernels, Bernhard Scholkopf.

This course covers the basics for Support Vector Machines and related Kernel methods. This course has six lectures.

Course Outline:

Kernel and Feature Spaces, Large Margin Classification, Basic Ideas of Learning Theory, Support Vector Machines, Other Kernel Algorithms.

10. Kernel Methods, Alexander Smola, Australian National University.  This is an advanced course as compared to the above and covers exponential families, density estimation, and conditional estimators such as Gaussian Process classification, regression, and conditional random fields, Moment matching techniques in Hilbert space that can be used to design two-sample tests and independence tests in statistics.

11. *Introduction to Kernel Methods, Bernhard Scholkopf, There are four parts to this course.

Course Outline:

Kernels and Feature Space, Large Margin Classification, Basic Ideas of Learning Theory, Support Vector Machines, Examples of Other Kernel Algorithms.

12. Introduction to Kernel Methods, Partha Niyogi.

13. Introduction to Kernel Methods, Mikhail Belkin, Ohio State University.This lecture is second in part to the above.

14. *Kernel Methods in Statistical Learning, John-Shawe Taylor.

15. *Support Vector Machines, Chih-Jen Lin, National Taiwan University. Easily one of the best talks on SVM. Almost like a run-down tutorial.

Course Outline:

Basic concepts for Support Vector Machines, training and optimization procedures of SVM, Classification and SVM regression.

16. *Kernel Methods and Support Vector Machines, Alexander Smola. A comprehensive six lecture course.

Course Outline:

Introduction of the main ideas of statistical learning theory, Support Vector Machines, Kernel Feature Spaces, An overview of the applications of Kernel Methods.

—

Additional Courses:

1. Basics of Probability and Statistics for Machine Learning, Mikaela Keller.

This course covers most of the basics that would be required for the above courses. However sometimes the shooting quality is a little shady. This talk seems to be the most popular on the video lectures site, one major reason in my opinion is that the lady delivering the lecture is quite pretty!

2. Some Mathematical Tools for Machine Learning, Chris Burges.

3. Machine Learning Laboratory, S.V.N Vishwanathan.

4. Machine Learning Laboratory, Chrisfried Webers.

—

Introductory Tutorials (PDF/PS):

1. *Support Vector Machines with Applications (Statistical Science). Click here >>

2. *Support Vector Machines (Marti Hearst, UC Berkeley). Click Here >>

3. *Support Vector Machines- Hype or Hallelujah (K. P. Bennett, RPI). Click Here >>

4. Support Vector Machines and Pattern Recognition (Georgia Tech). Click Here >>

5. An Introduction to Support Vector Machines in Data Mining (Georgia Tech). Click Here >>

6. University of Wisconsin at Madison CS 769 (Zhu). Click Here >>

7. Generalized Support Vector Machines (Mangasarian, University of Wisconsin at Madison). Click Here >>

8. *A Practical Guide to Support Vector Classification (Hsu, Chang, Lin, Via U-Michigan Ann Arbor). Click Here >>

9. *A Tutorial on Support Vector Machines for Pattern Recognition (Christopher J.C Burges, Bell Labs Lucent Technologies, Data mining and knowledge Discovery). Click Here >>

10. Support Vector Clustering (Hur, Horn, Siegelmann, Journal of Machine Learning Research. Via MIT). Click Here >>

11. *What is a Support Vector Machine (Noble, MIT). Click Here >>

12. Notes on PCA, Regularization, Sparisty and Support Vector Machines (Poggio, Girosi, MIT Dept of Brain and Cognitive Sciences). Click Here >>

13. *CS 229 Lecture Notes on Support Vector Machines (Andrew Ng, Stanford University). Click Here >>

—

Introductory Slides (mostly lecture slides):

1. Support Vector Machines in Machine Learning (Arizona State University). Click here >>

Lecture Outline:

What is Machine Learning, Solving the Quadratic Programs, Three very different approaches, Comparison on medium and large sets.

2. Support Vector Machines (Arizona State University). Click Here >>

Lecture Outline:

The Learning Problem, What do we know about test data, The capacity of a classifier, Shattering, The Hyperplane Classifier, The Kernel Trick, Quadratic Programming.

3. Support Vector Machines, Linear Case (Jieping Ye, Arizona State University). Click Here >>

Lecture Outline:

Linear Classifiers, Maximum Margin Classifier, SVM for Separable data, SVM for non-separable data.

4. Support Vector Machines, Non Linear Case (Jieping Ye, Arizona State University). Click Here >>

Lecture Outline:

Non Linear SVM using basis functions, Non-Linear SVMs using Kernels, SVMs for Multi-class Classification, SVM path, SVM for unbalanced data.

5. Support Vector Machines (Sue Ann Hong, Carnegie Mellon). Click Here >>

6. Support Vector Machines (Carnegie Mellon University Machine Learning 10701/15781). Click Here >>

7. Support Vector Machines and Kernel Methods (CMU). Click Here >>

8. SVM Tutorail (Columbia University). Click Here >>

9. Support Vector Machines (Via U-Maryland at College Park). Click Here >>

10. Support Vector Machines: Algorithms and Applications (MIT OCW). Click Here >>

11. Support Vector Machines (MIT OCW). Click Here >>

—

Papers/Notes on some basic related ideas (No estoric research papers here):

1. Robust Feature Induction for Support Vector Machines (Arizona State University). Click Here >>

2. Hidden Markov Support Vector Machines (Brown University). Click Here >>

3. *Training Data Set for Support Vector Machines (Brown University). Click Here >>

4. Support Vector Machines are Universally Consistent (Journal Of Complexity). Click Here >>

5. Feature Selection for Classification of Variable Length Multi-Attribute Motions (Li, Khan, Prabhakaran). Click Here >>

6. Selecting Data for Fast Support Vector Machine Training (Wang, Neskovic, Cooper). Click Here >>

7. *Normalization in Support Vector Machines (Caltech). Click Here >>

8. The Support Vector Decomposition Machine (Periera, Gordon, Carnegie Mellon). Click Here >>

9. Semi-Supervised Support Vector Machines (Bennett, Demiriz, RPI). Click Here >>

10. Supervised Clustering with Support Vector Machines (Finley, Joachims, Cornell University). Click Here >>

11. Metric Learning: A Support Vector Approach (Cornell University). Click Here >>

12. Training Linear SVMs in Linear Time (Joachims, Cornell Unversity). Click Here >>

13. *Rule Extraction from Linear Support Vector Machines (Fung, Sandilya, Rao, Siemens Medical Solutions). Click Here >>

14. Support Vector Machines, Reproducing Kernel Hilbert Spaces and Randomizeed GACV (Wahba, University of Wisconsian at Madison). Click Here >>

15. The Mathematics of Learning: Dealing with Data (Poggio, Girosi, AI Lab, MIT). Click Here >>

16. Training Invariant Support Vector Machines (Decoste, Scholkopf, Machine Learning). Click Here >>

—

*As I have already mentioned above, the star marked courses/lectures/tutorials/papers are the ones that I have seen and studied from personally (and hence can vouch for) and these in my opinion should work best for beginners.

Onionesque Reality Home >>

Read Full Post »