I have been involved in a major project on contrast enhancement of Magnetic Resonance Images by using Independent Component Analysis (ICA) and Support Vector Machines (SVM) for the past couple of months. It is an extremely exciting project and also something new for me, as I have worked on bio-medical images just once before. In the past, I have used ICA and SVM in face recognition/authentication, however this application is quite novel.
This post intends to introduce the problem, discuss a motivating example, some methods, expected work and some problems.
__________
A Simple Introduction and Motivating Example:
The simplest motivating example for this problem is the famous cocktail party problem:
You are at a cocktail party, and there are about 12 people present with each talking simultaneously. Add to that a music source. So that makes it 13.
Suppose you want to follow what each person was saying later and for doing so you place a number of tape recorders at different locations in the room (let’s not worry about the number of recorders right now). When you hear them later, the sounds would hardly be understandable as they would be mixed up.
Now you define an engineering problem : that using these recordings (which are basically mixtures), separate out the different sources with as little distortion as possible. In a real time cocktail party, the brain shows[1][2][3] a remarkable ability to follow one conversation. However such a problem has proved to be quite difficult in signal processing. Let’s just illustrate the cocktail party problem in a cartoon below :

The Cocktail Party Problem
Please listen to a demo of the cocktail party problem at the HUT ICA project page.
__________
The Logic Behind Constructing MR Images in Simple Terms:
Now, keeping the previous brief discussion in mind. Let’s introduce in simple words how MRI works. This is just a simplification to make the idea clearer, and not really how MRI works. Discussing MRI in detail would divert the focus of the post. To look at how MRI works follow these highly recommended tutorials[4][5][6]:
Suppose your body is placed in a Magnetic Field (let’s not worry about specifics yet). Consider two contiguous tissues in your body – X and Y. When subject to a magnetic field, the particles (protons) in the tissues would get aligned according to the field. The amount of magnetization would depend on the tissue type. Now suppose we want to measure how much a tissue gets magnetized. One way to think about it is like this : First apply the magnetic field, after the application the particles would get excited. Once the field is removed, these particles would tend to relax to their ground state. By being able to measure the time it takes for the particles to return, we would get some measure of the magnetization of the tissue(s). This is because, the greater the time for relaxation, greater the magnetization.
An image is basically a measure of the energy distribution. Now suppose we have the measurements for tissues X and Y, and since they were of a different nature (composition, density of protons etc), their response to the field would have been different. Thus we would get some contrast between them and thus would get an image.
In very simplistic terms, this is how MRI scans are obtained. Though as mentioned above, please follow [4][5][6] for detailed tutorials on MRI.
__________
MRI scans of the Brain and the Cocktail Party Problem :
Now consider the above discussion in context of taking a MRI scan of the brain. The brain has a number of constituents. Some being : Gray Matter, White Matter, Cerebrospinal Fluid (CSF) Fat, Muscle/Skin, Glial Matter etc. Now since each is unique, they would exhibit unique characteristics under a magnetic field. However, while taking a scan, we get one MRI image of the entire brain.
These scans can be considered as an equivalent to the mixtures of the cocktail party example. If we apply blind source separation to these, we should be able to separate out the various constituents such as gray matter, white matter, CSF etc. These images of the independent sources can be used for better diagnosis. This would be something like this :
If suppose the Simulated MR scans (from the McGill Simulated brain Database) were as follows:

Simulated MR Scans
The “ground truth” images for these scans would be as follows :

Ground Truth Images of Different Brain Tissue Substances
__________
Restatement of the Broad Research Problem and Use of ICA and SVM:
Magnetic Resonance Imaging is superior to Computerised Tomography for brain imaging at least, for the reason that it can give much better soft tissue contrast (because even small changes in the proton density and composition in the tissue are well represented).
Like for most techniques, improvements to scans obtained by MRI are much desired to improve diagnosis. Blind source separation has been used to separate physiologically different components from EEG[7]/MEG[8] data (similar to the cocktail party problem), financial data[9] and even in fMRI[10][11]. But it has not received much attention for MRI. Nakai et al[12] used Independent Component Analysis for the purpose of separating physiologically independent components from MRI scans. They took MR images of 10 normal subjects, 3 subjects with brain tumour and 1 subject with multiple sclerosis and performed ICA on the data. They reported success in improving contrast for gray and white matter, which was beneficial for the diagnosis of brain tumour. The demylination in Multiple sclerosis cases was also enhanced in the images. They suggested that ICA could potentially separate out all the tissues which had different relaxation characteristics (different sources of the cocktail party example). This approach thus shows much promise.
In more technical terms : Consider a set of MR frames as a single multispectral image. Where each band is taken during a particular pulse sequence (will be discussed below). Then use ICA on the data to separate out the physiologically independent components. A classifier such as the SVM can improve the contrast further of the separated independent components.
However, using ICA for MRI has been tricky, something I would discuss towards the end of this post and also in future posts.
Before doing so, I intend to touch up on the basics for the sake of completeness.
__________
Magnetic Resonance Imaging:
I had been thinking of writing a detailed tutorial on MRI, mostly because it requires some basic physics. However I don’t think it is required. I would recommend [4][5][6] for a study of the same in sufficient depth. I have recently taken tutorials on MRI, and would be willing to write for the blog if there are requests.
__________
An Introduction to Independent Component Analysis:
Independent Component Analysis was developed initially to solve problems such as the cocktail party problem discussed above.
Let’s formalize a problem like the cocktail party example. For simplicity let us assume that there are only two sources and two mixtures (obtained by keeping two recorders at different locations in the party).
Let’s represent these two mixtures as 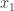 and
and  , and let
, and let 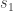 and
and 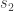 be the two sources that were mixed. Since we are assuming that the two microphones were kept at different locations, the mixtures
be the two sources that were mixed. Since we are assuming that the two microphones were kept at different locations, the mixtures 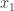 and
and  would be different.
would be different.
We could write this as:


The coefficients 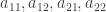 are basically some parameters that depend on the distance of the respective source from the microphones.
are basically some parameters that depend on the distance of the respective source from the microphones.
Let’s define our problem as : Using only the mixtures  estimate the signal sources
estimate the signal sources 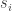 . It is notable that you do not have any knowledge of the parameters
. It is notable that you do not have any knowledge of the parameters  .
.
This could be illustrated by this :
Consider three signals:
 Suppose we have five mixtures obtained from these three signals.
Suppose we have five mixtures obtained from these three signals.

Signals obtained by mixing source signals
If you only have the mixed signals available. And do not know how they were mixed (parameters  not known). And from these mixed signals (
not known). And from these mixed signals (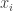 ) you have to estimate the source signals (
) you have to estimate the source signals ( ). This problem is of considerable difficulty.
). This problem is of considerable difficulty.
One approach would be : Use the statistical properties of the signals (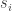 ) to estimate the parameters (
) to estimate the parameters ( ). It is surprising that it is enough to assume that
). It is surprising that it is enough to assume that 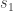 and
and 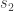 are statistically independent. This assumption might not be valid in many scenarios. But works well in most situations.
are statistically independent. This assumption might not be valid in many scenarios. But works well in most situations.
We could write the above system of linear equations in matrix form as :

where,  represents the mixing matrix,
represents the mixing matrix,  and
and  represent the mixtures and the sources respectively.
represent the mixtures and the sources respectively.
The problem is to estimate  from
from  without knowing
without knowing  . The assumption made is that the sources
. The assumption made is that the sources  are statistically independent.
are statistically independent.
How we go about solving this problem is exciting and an area of active research. ICA was originally developed for solving such problems. Please follow [12][13][14] for discussions on mutual information, measures of non-gaussianity such as Kurtosis and Negentropy and the fastICA algorithm.
__________
Why can ICA be used in MRI?
One limitation that ICA faces is that it can not work if more than one signal sources have a Gaussian distribution. This can be illustrated as follows:
Again consider our equation for just two sources :
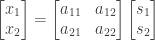
Our problem was : We have to estimate  from
from  without any knowledge of
without any knowledge of  . We would first need to estimate the parameters
. We would first need to estimate the parameters  from
from  , assuming statistical independence of
, assuming statistical independence of  . And then we could find
. And then we could find  as :
as :
 , where
, where  , or the inverse of the estimated mixing matrix
, or the inverse of the estimated mixing matrix  .
.
To understand how a solution would become impossible if both the sources had a Gaussian distribution, consider this :
Consider two independent components having the following uniform distributions:

The joint density of the two sources would then be uniform on a square. This follows from the fact that the joint density would be the product of the two marginal densities.

The joint distribution for Si
[ Image Source : Reference [12][13] ]
Now if 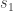 and
and 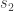 were mixed by a mixing matrix
were mixed by a mixing matrix 

The mixtures obtained are 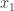 and
and  . Now since the original sources had a joint distribution on a square, and they were transformed by using a mixing matrix, the joint distribution of the mixtures
. Now since the original sources had a joint distribution on a square, and they were transformed by using a mixing matrix, the joint distribution of the mixtures 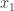 and
and  will be a parallelogram. These mixtures are no longer independent.
will be a parallelogram. These mixtures are no longer independent.

Joint Distribution of the mixtures
[ Image Source : Reference [12][13] ]
Now consider the problem once again : We have to estimate the mixing matrix  from the mixtures
from the mixtures  , and using this estimated
, and using this estimated  we have to estimate the sources
we have to estimate the sources 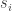 .
.
From the above joint distribution we have a way to estimate  . The edges of the parallelogram are in a direction given by the columns of
. The edges of the parallelogram are in a direction given by the columns of  . This is an intuitive way of estimating the mixing matrix : obtain the joint distributions of the mixtures, estimate the columns of the mixing matrix by finding the directions of the edges of the parallelogram. This solution gives a good intuitive feel of a in-principle solution of the problem( however, it isn’t practical).
. This is an intuitive way of estimating the mixing matrix : obtain the joint distributions of the mixtures, estimate the columns of the mixing matrix by finding the directions of the edges of the parallelogram. This solution gives a good intuitive feel of a in-principle solution of the problem( however, it isn’t practical).
However, now instead of two independent sources having a uniform distribution consider two independent sources having a Gaussian distribution. The joint distribution would be :

Joint Distribution when both Independent sources are Gaussian
[ Image Source : Reference [12][13] ]
Now going by the above discussion, because of the nature of the above joint distribution, it is not possible to estimate the mixing matrix from it.
Thus ICA fails when one or more independent components have a a gaussian distribution.
Noise in MRI is non-gaussian[16], therefore ICA is suited for MRI.
__________
Problems in Using ICA for MRI Blind Source Separation:
The application of ICA for MRI faces a number of problems. I would discuss these in later blog posts. I would only discuss one major problem – the problem of Over-Complete ICA.
Over-Complete ICA in MRI:
The problem of over complete ICA occurs when there are lesser sensors (tape recorders from our above discussion) than sources. This problem can be understood by the following discussion. Suppose you have 3 mixtures 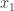 ,
,  and
and 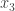 (imagine you have collected 3 tape recordings in a cocktail party of 6). Therefore you now have to estimate 6 sources from 3 mixtures.
(imagine you have collected 3 tape recordings in a cocktail party of 6). Therefore you now have to estimate 6 sources from 3 mixtures.
Now the problem becomes something like this :


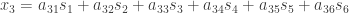
Assume for a second we can still estimate  , still we can not find all the signal sources. As the number of linear equations is just three, while the number of unknowns is 6. This is a considerably harder problem and has been discussed by many groups such as [19][20][21].
, still we can not find all the signal sources. As the number of linear equations is just three, while the number of unknowns is 6. This is a considerably harder problem and has been discussed by many groups such as [19][20][21].
Now dropping our assumption, the estimation of  is also harder in such a case.
is also harder in such a case.
The Case in MRI:
The problem of over-complete ICA doesn’t arise when it comes to functional-MRI. However it is a problem when it comes to MRI[17].
In MRI, by varying the parameters used for imaging, the three kind of images that can be obtained are T1 weighted, T2 weighted and Proton Density images. Going by our discussion in the section on MRI above. These three can be treated as mixtures.
Therefore, we have 3 mixtures at our disposal. However, as the ground truth images above show: The number of different tissues in the brain exceeds 9. Thus this becomes a considerably difficult problem : We have to estimate 9-10 independent components from just 3 mixtures.
I would discuss methods that can help do that in later blog posts.
If only three mixtures are used, 3 ICs can be estimated. Since the actual number of ICs exceeds 9. It is obvious that the each of 3 ICs have atleast 2 ICs mixed, which means that a certain tissue type is not enhanced as much as it could have been had there been one IC for it. This can be understood by looking at this example.

3 ICs obtained by Applying Fast-ICA on MR scans
[I used FastICA for obtaining these Independent Components ]
To get more ICs, in simple words, we need more mixtures. However we can obtain more mixtures from the existing mixtures itself by a process of Band-Expansion[18].
I would discuss this problem of OC-ICA and it’s possible solutions in later posts.
__________
To Conclude:
A basic idea related to application of ICA to MR scans was discussed. It is clear that even with just three ICs significant tissue contrast enhancement is achieved. Problems related to OC-ICA would be discussed in later posts one by one. I would also discuss quantifying the results obtained using the Tanimoto/Jaccard coefficient of similarity.
__________
References and Resources:
Cocktail Party Problem
[1] “Some Experiments on the Recognition of Speech, with One and with Two Ears“; E. Colin Cherry; The Journal of the Acoustical Society of America; September 1953. (PDF)
[2] “The Attentive Brain“; Stephen Grossberg; Department of Cognitive and Neural Systemss – Boston University; American Scientist, 1995. (PDF)
[3] “The Cocktail Party Problem : A Primer“; Josh H. McDermott; Current Biology Vol 19. No. 22. (PDF)
Magnetic Resonance Imaging
[4] “Magnetic Resonance ImagingTutorial“; H Panepucci and A Tannus; Technical Report; USP, 1994. (PDF)
[5] “10 Video lessons on MRI by Paul Callaghan” (~ an hour in total). (Videos)
[6] “MRI Tutorial for Neuroscience Boot Camp” Melissa Saenz. (PDF)
Sample ICA Applications Similar to The Cocktail Party Problem
[7] “Independent Component Analysis of Electroencephalographic Data“; Makieng, Bell, Jung, Sejnowski; Advances in Neural Information Processing Systems, 1996. (PDF)
[8] “Application of ICA to MEG noise Reduction“; Masaki Kawakatsu; 4th International Symposium on Independent Component Analysis and Blind Source Separation; 2003. (PDF)
[9] “Independent Component Analysis in Financial Data” from the book Computational Finance; Yasser S. Abu-Mostafa; The MIT Press; 2000. (Book Link)
[10] “ICA of functional MRI data : An overview“; Calhoun, Adali, Hansen, Larsen, Pekar; 4th International Symposium on Independent Component Analysis and Blind Source Separation; 2003. (PDF)
[11] “Independent Component Analysis of fMRI Data – Examining the Assumptions“; McKeown, Sejnowski; Human Brain Mapping; 1998. (PDF)
Independent Component Analysis : Tutorials/Books
[12] “Independent Component Analysis : Algorithms and Applications“; Aapo Hyvärinen, Erkki Oja; Neural Networks; 2000. (PDF)
[13] “Independent Component Analysis“; Aapo Hyvärinen, Juha Karhunen, Erkki Oja; John Wiley Publications; 2001. (Book Link)
[14] ICA Tutorial at videolectures.net by Aapo Hyvärinen. (Videos)
Independent Component Analysis for Magnetic Resonance Imaging
[15] “Application of of Independent Component Analysis to Magnetic Resonance Imaging for enhancing the Contrast of Gray and White Matter“; Nakai, Muraki, Bagarinao, Miki, Takehara, Matsuo, Kato, Sakahara, Isoda; NeuroImage; 2004. (Journal Link)
[16] “Noise in MRI“; Albert Macovski; Magnetic Resonance in Medicine; 1996. (PDF)
[17] “Independent Component Analysis in Magnetic Resonance Image Analysis“; Ouyang, Chen, Chai, Clayton Chen, Poon, Yang, Lee; EURASIP journal on Advances in Signal Processing; 2008 (Journal Link)
[18] “Band Expansion Based Over-Complete Independent Component Analysis for Multispectral Processing of Magnetic Resonance Images “; Ouyang, Chen, Chai, Clayton Chen, Poon, Yang, Lee; IEEE Transactions on Biomedical Imaging; June 2008. (PDF)
Over-Complete ICA:
[19] “Blind Source Separation of More Sources Than Mixtures Using Over Complete Representations“; Lee, Lewicki, Girolami, Sejnowski; IEEE Signal Processing Letters; 1999. (PDF)
[20] “Learning Overcomplete Representations“; Lewicki, Sejnowski. (PDF)
[21] “A Fast Algorithm for estimating over-complete ICA bases for Image Windows “; Hyvarinen, Cristescu, Oja; International Joint Conference on Neural Networks; 1999. (IEEE Xplore link)
__________
Onionesque Reality Home >>
Read Full Post »
.
.
will be Antoine’s necklace.