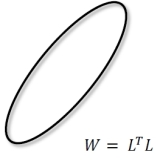Where does the Sigmoid in Logistic Regression come from?

Note: The title of this post is circular. But I use/abuse it because of the post linked below.

I noticed on the Hacker News front page (and via multiple reshares on twitter), a discussion on why logistic regression uses a sigmoid. The article linked in the story talks about the log-odds ratio, and how it leads to the sigmoid (and gives a good intuitive plug on it).

However, I think that the more important question is – Why do you care about log-odds? Why do you use log-odds and not something else? The point of this quick post is to write out why using the log-odds is infact very well motivated in the first place, and once it is modeled by a linear function, what you get is the logistic function.

Beginning with log-odds would infact be begging the question, so let us try to understand.

____________________________

To motivate and in order to define the loss etc, suppose we had a linear classifier: . This just means that for a vector input, we take the dot product with the parameters and take the sign.

The learning problem would be to figure out a good direction and a good location of the decision boundary .

____________________________

We want to figure these out so as to minimize the expected 0-1 loss (or expected number of mistakes) for the classifier . The 0-1 loss for a datapoint-label pair is simply:

Now, the next question we would like to ask. What is the risk of this classifier that we want to minimize? The risk is the expected loss. That is, if we draw a random sample from the (unknown) distribution , what would be the expected error? More concretely:

Writing out the expectation:

Using the chain rule this becomes:

It is important to understand this expression. This is not assuming anything about the data. However, it is this expression that we want to minimize if we want to get a good classifier. To minimize this expression, it suffices to simply minimize for the conditional risk for any point (i.e. the middle part of the above expression):

But this conditional risk can be written as:

Note that,

Therefore, the conditional risk is simply:

Now, it is this conditional risk that we want to minimize given a point . And in order to do so, looking at the expression above, the classifier must make the following decision:

It is again important to note that so far we have made absolutely no assumptions about the data. So the above classifier is the best classifier that we can have in terms of generalization, in the sense of what might be the expected loss on a new sample point. Such a classifier is called the Bayes Classifier or sometimes called the Plug-in classifier.

But the optimal decision rule mentioned above i.e. is equivalent to saying that:

by taking log, this would be:

If, we were only dealing with binary classification, this would imply:

Notice that by making no assumptions about the data, simply by writing out the conditional risk, the log-odds ratio has fallen out directly. This is not an accident, because the optimal bayes classifier has this form for binary classification. But the question still remains, how do we model this log-odds ratio? The simplest option is to consider a linear model (there is no reason to stick to a linear model, but due to some reasons, one being convexity, we stick to a linear model):

Now, we know that , plugging this in the above, and exponentiating, we have:

Rearranging, yields the familiar logistic model (and the sigmoid):

.

As noted in the post linked in the beginning, the logistic model, , which for any is, , and is monotonic .

____________________________

This derivation shows that the log-odds is not an arbitrary choice, infact a very natural choice. The sigmoid is simply a consequence of modeling the log-odds with a linear function (infact logistic regression is arguably the simplest example of a log-linear model, if we had structured outputs, a natural extension of such a model would be the Conditional Random Field. The choice of using a linear function is simply to make the optimization convex, amongst some other favourable properties).

____________________________

Note: This post was inspired by some very succinct notes by Gregory Shakhnarovich from his Machine Learning class, that I both took and served as a TA for.

A Note on the Graph Laplacian

A short note on how the Graph Laplacian is a natural analogue of the Laplacian in vector analysis.

For a twice differentiable function on the euclidean space, the Laplacian of , is the div(grad()) or the divergence of the gradient of . Let’s consider the laplacian in two dimensions:

To get an intuition about what it does, it is useful to consider a finite difference approximation to the above:

The above makes it clear that the Laplacian behaves like a local averaging operator. Infact the above finite difference approximation is used in image processing (say, when h is set to one pixel) to detect sharp changes such as edges, as the above is close to zero in smooth image regions.

____________________________

The finite difference approximation intuitively suggests that a discrete laplace operator should be natural. At the same time, the Graph Theory literature defines the Graph Laplacian as the matrix (where is the degree matrix and the adjacency matrix of the graph , both are defined below). It is not obvious that this matrix follows from the div(grad(f)) definition mentioned above. The purpose of this note is to explicate in short on how this is natural, once the notion of gradient and divergence operators have been defined over a graph.

First of all the two most natural matrices that can be associated with a graph are defined below:

____________________________

There are two natural matrices that are used to specify a simple graph with vertex set and edge set : The Adjacency matrix and the Incidence matrix .

The Adjacency matrix is defined as a matrix such that:

To define the incidence matrix , we need to fix an orientation of the edges (for our purpose an arbitrary orientation suffices), then:

Now suppose we have a real valued function over , . For , we view this as a column vector indexed by the vertices.

Similarly let be a real valued function over the edges , (again, we view this as a row vector indexed by the edges).

Now, consider the following map: (which is now a vector indexed by ). The value of this map at any edge is simply the difference of the values of at the two end points of the edge i.e. . This makes it somewhat intuitive that the matrix is some sort of a difference operator on . Given this “difference operator” or “discrete differential” view, can then be viewed as the gradient that measures the change of the function along the edges of . Thus the map is just the gradient operator.

Like the above, now we consider the following map: (which is now a vector indexed by ). Recall that was defined on the edges. The value of this map at any vertex is . If we were to view as describing some kind of a flow on the edges, then is the net outbound flow on the vertex , which is just the divergence. Thus the map  is just the divergence operator.

Now consider (note that this makes sense since is a column vector), going by the above, this should be the divergence of the gradient. Thus, the analogy with the “real” Laplacian makes sense and the matrix is appropriately called the Graph Laplacian.

Using the definition of , a simple computation yields the following for :

Looking at the above and recalling the definition for the adjacency matrix , it is easy to see that , where is the diagonal matrix with . This is just the familiar definition that I mentioned at the start.

PS: From the above it is also clear that the Laplacian is positive semidefinite. Indeed, consider , which is written as

From Eros to Gaia

I had been re-reading “From Eros to Gaia” by Freeman Dyson after some years. I have a bad habit of never reading prefaces to books, however I am glad I read it this time around because of this sobering passage that appears in it:

My mother used to say that life begins at forty. That was her age when she had her first baby. I say, on the contrary, that life begins at fifty-five, the age when I published my first book. So long as you have courage and a sense of humour, it is never too late to start life afresh. A book is in many ways like a baby. While you are writing, it is curled up in your belly. You cannot get a clear view of it. As soon as it is born, it goes out into the world and develops a character of its own. Like a daughter coming home from school, it surprises you with unexpected flashes of wisdom. The same thing happens with scientific theories. You sit quietly gestating them, for nine months or whatever the required time may be, and then one day they are out on their own, not belonging to you anymore but to the whole community of scientists. Whatever it is that you produce– a baby, a book, or a theory– it is a piece of the magic of creation. You are producing something that you do not fully understand. As you watch it grow, it becomes part of a larger world, and fits itself into a larger design than you imagined. You belong to the company of those medieval craftsmen who added a carved stone here or a piece of scaffolding there, and together built Chartres Cathedral.

Neighbourhood Gerrymandering: An Approach to Discriminative Metric Learning via Latent Structured Prediction

An informal summary of a recent project I had some involvement in.

Motivation: Why care about Metric Learning?

In many machine learning algorithms, such as k-means, Support Vector Machines, k-Nearest Neighbour based classification, kernel regression, methods based on Gaussian Processes etc etc – there is a fundamental reliance, that is to be able to measure dissimilarity between two examples. Usually this is done by using the Euclidean distance between points (i.e. points that are closer in this sense are considered more similar), which is usually suboptimal in the sense that will be explained below. Being able to compare examples and decide if they are similar or dissimilar or return a measure of similarity is one of the most fundamental problems in machine learning. Ofcourse a related question is: What does mean by “similar” afterall?

To illustrate the above let us work with k-Nearest Neighbour classification. Before starting, let us just illustrate the really simple idea (of kNN classification) by an example: Consider the following points in 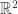, with the classes marked by different colours.

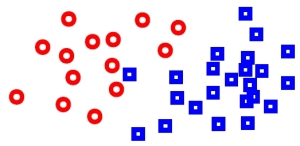
Now suppose we have a new point – marked with black – whose class is unknown. We assign it a class by looking at the nearest neighbors and taking the majority vote:

Some notes on kNN:

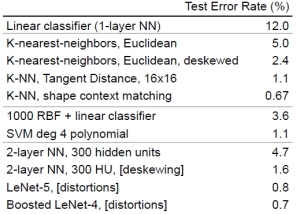
A brief digression first before moving on the problem in the above (what is nearest?). kNN classifiers are very simple and yet in many cases they can give excellent performance. For example, consider the performance on the MNIST dataset, it is clear that kNN can give competitive performance as compared to other more complicated models.

Moreover, they are simple to implement, use local information and hence are inherently nonlinear. The biggest advantage in my opinion is that it is easy to add new classes (since no retraining from scratch is required) and since we average across points, kNN is also relatively robust to label noise. It also has some attractive theoretical properties: for example kNN is universally consistent (as the number of points approaches infinity, with appropriate choice of k, the kNN error will approach the Bayes Risk).

Notion of “Nearest”:

At the same time, kNN classifiers also have their disadvantages. One is related to the notion of “nearest” (which falls back on what was talked about at the start) i.e. how does one decide what points are “nearest”. Usually such points are decided on the basis of the Euclidean distance on the native feature space which usually has shortfalls. Why? Because nearness in the Euclidean space may not correspond to nearness in the label space i.e. points that might be far off in the Euclidean space may have similar labels. In such cases, clearly the notion of “near” using the euclidean distance is suboptimal. This is illustrated by a set of figures below (adapted from slides by Kilian Weinberger):

An Illustration:

Consider the image of this lady – now how do we decide what is more similar to it?

 

Someone might mean similar on the basis of the gender:

Or on the basis of age:

Or on the basis of the hairstyle!

Similarity depends on the context! Something that the euclidean distance in the native feature space would fail to capture. This context is provided by labels.

Distance Metric Learning:

The goal of Metric Learning is to learn a distance metric, so that the above label information is incorporated in the notion of distance i.e. points that are semantically similar are now closer in the new space. The idea is to take the original or native feature space, use the label information and then amplify directions that are more informative and squish directions that are not. This is illustrated in this figure – notice that the point marked in black would be incorrectly classified in the native feature space, however under the learnt metric it would be correctly classified.

It is worthwhile to have a brief look at what this means. The Euclidean distance (with ) is defined by

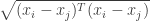
as also was evident in the above figure, this corresponds to the following euclidean ball in 2-D

A family of distance measure may be defined using an inner product matrix. These are called the Mahalanobis metrics.

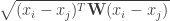
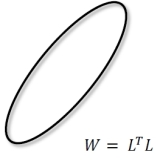
The learnt metric affects a rescaling and rotation of the original space. The goal is now to learn this using the label information so that the new distances correspond better to the semantic context. It is easy to see that when , the above is still a distance metric.

Learning :

Usually the real motivation for metric learning is to optimize for the kNN objective i.e. learn the matrix 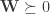so that the kNN error is reduced. But note that directly optimizing for the kNN loss is intractable because of the combinatorial nature of the optimization (we’ll see this in a bit), so instead, is learnt as follows:

1. Define a set of “good” neighbors for each point. The definition of “good” is usually some combination of proximity to the query point and label agreement between the points.

2. Define a set of “bad” neighbours for each point. This might be a set of points that are “close” to the query point but disagree on the label (i.e. inspite of being close to the query point they might give a wrong classification if they were chosen to classify the query point).

3. Set up the optimization problem for such that for each query point, “good” neighbours are pulled closer to it while “bad” neighbours are pushed farther away, and thus learn so as to minimize the leave one out kNN error.

The exact formulation of “good” and “bad” varies from method to method. Here are some examples:

In one of the earliest papers on distance metric learning by Xing, Ng, Jordan and Russell (2002) – good neighbors are similarly labeled k points. The optimization is done so that each class is mapped into a ball of fixed radius. However no separation is enforced between the classes. This is illustrated in the following figure (the query point is marked with an X, similarly labeled k points are moved into a ball of a fixed radius):

One problem with the above is that the kNN objective does not really require that similarly labeled points are clustered together, hence in a way it optimizes for a harder objective. This is remedied by the LMNN described briefly below.

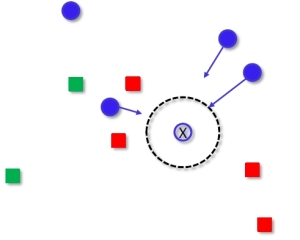
One of the more famous Metric Learning papers is the Large Margin Nearest Neighbors by Weinberger and Saul (2006). Here good neighbors are similarly labeled k points (and the circle around x is the distance of the farthest of the good neighbours) and “worst offenders” or “bad” neighbours are points that are of a different class but still in the nearest neighbors of the query point. The optimization is basically a semidefinite program that works to pull the good neighbours towards the query point and a margin is enforced by pushing the offending points out of this circle. Thus in a way, the goal in LMNN is to deform the metric in such a way that the neighbourhood for each point is “pure.

There are many approaches to the metric learning problem, however a few more notable ones are:

1. Neighbourhood Components Analysis (Goldberger, Roweis, Hinton and Salakhutdinov, 2004): Here the piecewise constant error of the kNN rule is replaced by a soft version. This leads to a non-convex objective that can be optimized by gradient descent. Basically, NCA tries to optimize for the choice  of neighbour at the price of losing convexity.

2. Collapsing Classes (Globerson and Roweis, 2006): This method attempts to remedy the non-convexity above by optimizing a similar stochastic rule while attempting to collapse each class to one point, making the problem convex.

3. Metric Learning to Rank (McFee and Lankriet, 2010): This paper takes a different take on metric learning, treating it as a ranking problem. Note that given a fixed p.s.d matrix a query point induces a permutation on the training set (in order of increasing distance). The idea thus is to optimize the metric for some ranking measure (such as precision@k). But note that this is not necessarily the same as requiring correct classification.

Neighbourhood Gerrymandering:

As a motivation we can look at the cartoon above for LMNN. Since we are looking to optimize for the kNN objective, the requirement to learn the metric should just be correct classification. Thus, we should need to push the points to ensure the same. Thus we can have the circle around x as simply the distance of the farthest point in the k nearest neighbours (irrespective of class). Now, we would like to deform the metric such that enough points are pulled in and pushed out of this circle so as to ensure correct classification. This is illustrated below.

This method is akin to the common practice of Gerrymandering, in drawing up borders of election districts so as to provide advantages to desired political parties. This is done by concentrating voters from a particular party and/or by spreading out voters from other parties. In the above, the “districts” are cells in the Voronoi diagram defined by the Mahalanobis metric and “parties” are class labels voted for by each neighbour.

 Motivations and Intuition:

Now we can step back a little from the survey above, and think a bit about the kNN problem in somewhat more precise terms so that the above approach can be motivated better.

For kNN, given a query point and a fixed metric, there is an implicit latent variable: The choice of the k “neighbours”.

Given this latent variable – inference of the label for the query point is trivial – since it is just the majority vote. But notice that for any given query point, there can exist a very large number of  choices of k points that may correspond to correct classification (basically any set of points with majority of correct class will work). Now we basically want to learn a metric so that we prefer one of these sets over any set of k neighbours which would vote for a wrong class. In particular, from the sets that affects correct classification we would like to pick the set that is on average most similar to the query point.

We can write kNN prediction as an inference problem with a structured latent variable being the choice of k neighbours.

The learning then corresponds to  minimizing a sum of structured latent hinge loss and a regularizer. Computing the latent hinge loss involves loss-augmented inference – which is basically looking for the worst offending k points (points that have high average similarity with the query point, yet correspond to a high loss). Given the combinatorial nature of the problem, efficient inference and loss-augmented inference is key. Optimization can basically be just gradient descent on the surrograte loss. To make this a bit more clear, the setup is described below:

Problem Setup:

Suppose we are given training examples that are represented by a “native” feature map, 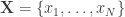with with class labels with , where stands for the set .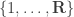

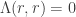Suppose are also provided with a loss matrix with being the loss incurred by predicting when the correct class is . We assume that and .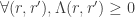

Now let 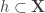be a set of examples in .

As stated earlier, we are interested in the Mahalanobis metrics:

For a fixed we may define the distance of 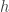with respect to a point as:

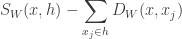
Therefore, the set of k-Nearest Neighbours of in is:

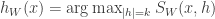
For any set of examples from we can predict the label of by a simple majority vote.

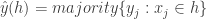
The kNN classifier therefore predicts .

Thus, the classification loss incurred using the set 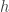can be defined as:

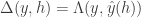
Learning and Inference:

One might want to learn so as to minimize the training loss:

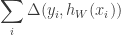
However as mentioned in passing above, this fails because of the intractable nature of  the classification loss . Thus we’d have to resort to the usual remedy: define a tractable surrograte loss.

It must be stressed again that the output of prediction is a structured object . The loss in structured prediction penalizes the gap between score of the correct structured output and the score of the “worst offending” incorrect output. This leads to the following definition of the surrogate:

This corresponds to our earlier intuition on wanting to learn such that the gap between the “good neighbours” and “worst offenders” is increased.

So, although the loss above was arrived at by intuitive arguments, it turns out that our problem is an instance of a familiar type of problem: Latent Structured Prediction and hence the machinery for optimization there can be used here as well. The objective for us corresponds to:

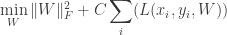
Where 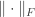is the Frobenius norm.

Note that the regularizer is convex, but the loss is not convex to the subtraction of the max term i.e. now it is a difference of convex functions which means the concave convex procedure may be used for optimization (although we just use stochastic gradient descent). Also note that the optimization at each step needs an efficient subroutine to determine the correct structured output (inference of the best set of neighbours) and the worst offending incorrect structured output (loss augmented inference i.e. finding the worst set of neighbors). Turns out that for this problem this is possible (although not presented here).

It is interesting to think about how this approach extends to regression and to see how it works when the embeddings learnt are not linear.

The Jacobian Inner Product

This post may be considered an extension of the previous post.

The setup and notation is the same as in the previous post (linked above). But to summarize: Earlier we had an unknown smooth regression function . The idea was to estimate at each training point, the gradient of this unknown function , and then taking the sample expectation of the outerproduct of the gradient. This quantity has some interesting properties and applications.

However it has its limitations, for one, the mapping restricts the Gradient Outer Product being helpful for only regression and binary classification (since for binary classification the problem can be thought of as regression). It is not clear if a similar operator can be constructed when one is dealing with classification, that is the unknown smooth function is a vector valued function where is the number of classes (let us say for the purpose of this discussion, that for each data point we have a probability distribution over the classes, a dimensional vector).

In the case of the gradient outer product since we were working with a real valued function, it was possible to define the gradient at each point, which is simply:

For a vector valued function , we can’t have the gradient, but instead can define the Jacobian at each point:

Note that may be estimated in a similar manner as estimating gradients as in the previous posts. Which leads us to define the quantity .

The first thing to note is that defined in the previous post is simply the quantity for the special case when . Another note is also in order: The reason why we suffixed that quantity with “outer product” (as opposed to “inner product” here) is simply because we considered the gradient to be a column vector, otherwise they are similar in spirit.

Another thing to note is that it is easy to see that the quantity is a positive semi-definite matrix and hence is a Reimannian Metric, which is defined below:

Definition: A Reimannian Metric on a manifold is a symmetric and positive semi-definite matrix, which defines a smoothly varying inner product in the tangent space , for each point and . This associated p.s.d matrix is called the metric tensor. In the above case, since is p.s.d it defines a Reimannian metric:

Thus, is a specific metric (more general metrics are dealt with in areas such as metric learning).

Properties: We saw some properties of in the previous post. In the same vein, does have similar properties? i.e. does the first eigenvector also correspond to the direction of highest average variation? What about the -dimensional subspace? What difference does it make that we are looking at a vector valued function? Also what about the cases when and otherwise?

These are questions that I need to think about and should be the topic for a future post to be made soon, hopefully.

The Gradient Outer Product

Recently, in course of a project that I had some involvement in, I came across an interesting quadratic form. It is called in the literature as the Gradient Outer Product. This operator, which has applications in supervised dimensionality reduction, inverse regression and metric learning can be motivated in two (related) ways, but before doing so, the following is the set up:

Setup: Suppose we have the usual set up as for nonparametric regression and (binary) classification i.e. let for some unknown smooth , the input is dimensional

1. Supervised Dimensionality Reduction: It is often the case that varies most along only some relevant coordinates. This is the main motivation behind variable selection.

The idea in variable selection is the following: That may be written as where . projects down the data to only relevant coordinates (i.e. some features are selected by while others are discarded).

This idea is generalized in Multi-Index Regression, where the goal is to recover a subspace most relevant to prediction. That is, now suppose the data varies significantly along all coordinates but it still depends on some subspace of smaller dimensionality. This might be achieved by letting from the above to be . It is important to note that is not any subspace, but rather the -dimensional subspace to which if the data is projected, the regression error would be the least. This idea might be further generalized by means of mapping to some non-linearly, but for now we only stick to the relevant subspace.

How can we recover such a subspace?

________________

2. Average Variation of : Another way to motivate this quantity is the following: Suppose we want to find the direction in which varies the most on average, or the direction in which varies the second fastest on average and so on. Or more generally, given any direction, we want to find the variation of along it. How can we recover these?

________________

The Expected Gradient Outer Product:  The expected gradient outer product of the unknown classification or regression function is the quantity:

The expected gradient outer product recovers the average variation of in all directions. This can be seen as follows: The directional derivative at along is given by or .

From the above it follows that if does not vary along then must be in the null space of .

Infact it is not hard to show that the relevant subspace as defined earlier can also be recovered from . This fact is given in the following lemma.

Lemma: Under the assumed model i.e. , the gradient outer product matrix is of rank at most . Let be the eigenvectors of corresponding to the top eigenvalues of . Then the following is true:

This means that a spectral decomposition of recovers the relevant subspace. Also note that the Gradient Outer Product corresponds to a kind of a supervised version of Principal Component Analysis.

________________

Estimation: Ofcourse in real settings the function is unknown and we are only given points sampled from it. There are various estimators for , which usually involve estimation of the derivatives. In one of them the idea is to estimate, at each point a linear approximation to . The slope of this approximation approximates the gradient at that point. Repeating this at the sample points, gives a sample gradient outer product. There is some work that shows that some of these estimators are statistically consistent.

________________

Related: Gradient Based Diffusion Maps: The gradient outer product can not isolate local information or geometry and its spectral decomposition, as seen above, gives only a linear embedding. One way to obtain a non-linear dimensionality reduction would be to borrow from and extend the idea of diffusion maps, which are well established tools in semi supervised learning. The central quantity of interest for diffusion maps is the graph laplacian , where is the degree matrix and the adjacency matrix of the nearest neighbor graph constructed on the data points. The non linear embedding is obtained by a spectral decomposition of the operator or its powers .

As above, a similar diffusion operator may be constructed by using local gradient information. One such possible operator could be:

Note that the first term is the same that is used in unsupervised dimension reduction techniques such as laplacian eigenmaps and diffusion maps. The second term can be interpreted as a diffusion on function values. This operator gives a way for non linear supervised dimension reduction using gradient information.

The above operator was defined here, however no consistency results for the same are provided.

Also see: The Jacobian Inner Product.

________________

Implementation and Abstraction in Mathematics

I recently noticed on arXiv that the following manuscript “Implementation and Abstraction in Mathematics” by David McAllester. A couple of years ago, I had taken a graduate course taught by David that had a similar flavour (the material in the manuscript is more advanced, in particular the main results, not to mention it is better organized and the presentation more polished), presenting a type theoretic foundation of mathematics. Although I can’t say I did very well in the course, I certainly enjoyed the ideas in it very much, and thus the above manuscript might be worth a look. Perhaps it might be a good idea to audit that course again, just to make sure I understand the main ideas better this time. :)

The Evolution of Programming Languages

I found these images on twitter via (Paige Bailey) @DynamicWebPaige  Found them so hilarious that I thought they deserved a blog post (Needless to say, click on each image for a higher resolution version).

PS: A quick search indicates that these are from “Land of Lisp: Learn to Program in List, One Game at a time” by M. D. Conrad Barski.

The 40s and 50s

60s and 70s

80s and 90s

2000

On the two notions of “Information”

Recently I was going through Shannon’s original 1948 Information Theory paper and a paper by Kolmogorov from 1983 that places the differences between “Shannon Information” and “Algorithmic Information” in sharp relief. After much information diffusion over the past decades the difference is quite obvious and particularly interesting to contrast nonetheless. Nevertheless I found these two paragraphs from these two papers interesting, if for nothing then for historical reasons.

“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design.” (C. E. Shannon, A Mathematical Theory of Communication, 1948).

“Our definition of the quantity of information has the advantage that it refers to individual objects and not to objects treated as members of a set of objects with a probability distribution given on it. The probabilistic definition can be convincingly applied to the information contained, for example, in a stream of congratulatory telegrams. But it would not be clear how to apply it, for example, to an estimate of the quantity of information contained in a novel or in the translation of a novel into another language relative to the original. I think that the new definition is capable of introducing in similar applications of the theory at least clarity of principle.” (A. N. Kolmogorov, Combinatorial Foundations of Information Theory and the Calculus of Probabilities, 1983).

Note the reference that Shannon makes is to a message selected from a set of possible messages (and hence the use of probability theory), his problem was mainly concerned with the engineering application of communication. While Kolmogorov talks of individual objects and is not directly concerned with communication and hence the usage of computability (the two notions are related ofcourse, for example the expected Kolmogorov Complexity is equal to Shannon entropy).

(Very) Informal thoughts on the No-Free-Lunch Theorem

The No-Free-Lunch theorems (Wolpert and Macready) are one of the mainstays in Machine Learning and optimization. Crudely, the NFL says that “for every learner there exists a distribution in which it fails”, giving a precise handle to reason about why a given learning algorithm might fail on certain tasks (or, “specialization” of a learning algorithm might just be accidental). It gives a good justification why it is useful to incorporate prior informaion about the problem at hand to perform better. Oftentimes the NFL is used to argue that a general purpose learning algorithm is theoretically impossible. This is incorrect. Indeed, universal learning algorithms exist and there is a (possibly very small) free lunch, at least for the case of “interesting problems” (thanks to Vick for pointing out these papers).

The view “for every learner there exists a distribution in which it fails” is very useful. However I had recently been thinking that is particularly instructive to think of No Free Lunch as a kind of diagnolization argument (this is just a different way of thinking about the prior statement). I am not completely sure if this works but it sounds plausible and makes me see NFL in a different light. It might also be that there is some subtle absrudity or flaw in this kind of thinking. However, I think the NFL theorem can be seen as a simple corollary of the following incompleteness theorem in Kolmogorov Complexity.

Theorem (Chaitin): There exists a constant L (which only depends on the particular axiomatic system and the choice of description language) such that there does not exist a string s for which the statement the “The Kolmogorov Complexity of s is greater than L” (as formalized in S) can be proven within the axiomatic system S. 

Stated informally: “There’s a number L such that we can’t prove the Kolmogorov complexity of any specific string of bits is more than L”. In particular, you can think of any learning machine as a compression scheme (since compression implies learning, we can think of any learning algorithm as a way to compress the data) of some fixed Kolmogorov Complexity (consider the most optimal program for that machine, the programming language is irrelevant as long as it is Turing Complete. Consider the description length of it in bits. That is its Kolmogorov Complexity). Now for any such learning machine (or class of learning machines w.l.o.g) you can construct a data string which has Kolmogorov Complexity greater than what this learning machine has. i.e. this data string is random from the point of view of this learning machine as it is incompressible for it. In short IF the data string has some Kolmogorov Complexity K and your learning machine has Kolmogorov Complexity k and k < K then you will never be able to find any structure in your data string i.e. can never show that it has a KC greater than k. Thus the data string given to our learner would appear to be structureless. Thus no free lunch is just a simple diagonalization argument in the spirit of incompleteness results. One can always construct a string that is Kolmogorov Random or structureless w.r.t our encoding scheme. Ofcourse the Kolmogorov Complexity is uncomputable. However I think the above argument works even when one is talking of upper bounds on the actual Kolmogorov Complexity, but I am not very sure about it or if there are any problems with it.

Also, if one assumes that that there is no reason to believe that structureless functions exist (if we assume that the data is generated by a computational process then there is probably no reason to believe that it is structureless i.e. the problem is “interesting”). And if this is the case, then you would always have a machine in your library of learning algorithms that will be able to find some upper bound on the Kolmogorov Complexity of the data string (much less than the machine itself). This search might be done using Levin’s universal search, for example. I think this line of reasoning leads naturally, to thinking why NFL doesn’t say anything about whether universal learning algorithms can exist.

PS: This thought train about NFL as diagonalization was inspired by a post by David McAllester on what he calls the “Free Lunch Theorem” over here. Some of this appeared as a comment there. However, now I have been inspired enough to study some of the papers concerned including his. (Unrelated to all this. I particularly found likening Chomsky’s Universal Grammar as simply an invocation of NFL on information theoretic grounds in his post very enlightening).