On the two notions of “Information”

Recently I was going through Shannon’s original 1948 Information Theory paper and a paper by Kolmogorov from 1983 that places the differences between “Shannon Information” and “Algorithmic Information” in sharp relief. After much information diffusion over the past decades the difference is quite obvious and particularly interesting to contrast nonetheless. Nevertheless I found these two paragraphs from these two papers interesting, if for nothing then for historical reasons.

“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point. Frequently the messages have meaning; that is they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design.” (C. E. Shannon, A Mathematical Theory of Communication, 1948).

“Our definition of the quantity of information has the advantage that it refers to individual objects and not to objects treated as members of a set of objects with a probability distribution given on it. The probabilistic definition can be convincingly applied to the information contained, for example, in a stream of congratulatory telegrams. But it would not be clear how to apply it, for example, to an estimate of the quantity of information contained in a novel or in the translation of a novel into another language relative to the original. I think that the new definition is capable of introducing in similar applications of the theory at least clarity of principle.” (A. N. Kolmogorov, Combinatorial Foundations of Information Theory and the Calculus of Probabilities, 1983).

Note the reference that Shannon makes is to a message selected from a set of possible messages (and hence the use of probability theory), his problem was mainly concerned with the engineering application of communication. While Kolmogorov talks of individual objects and is not directly concerned with communication and hence the usage of computability (the two notions are related ofcourse, for example the expected Kolmogorov Complexity is equal to Shannon entropy).

Read Full Post »

(Very) Informal thoughts on the No-Free-Lunch Theorem

The No-Free-Lunch theorems (Wolpert and Macready) are one of the mainstays in Machine Learning and optimization. Crudely, the NFL says that “for every learner there exists a distribution in which it fails”, giving a precise handle to reason about why a given learning algorithm might fail on certain tasks (or, “specialization” of a learning algorithm might just be accidental). It gives a good justification why it is useful to incorporate prior informaion about the problem at hand to perform better. Oftentimes the NFL is used to argue that a general purpose learning algorithm is theoretically impossible. This is incorrect. Indeed, universal learning algorithms exist and there is a (possibly very small) free lunch, at least for the case of “interesting problems” (thanks to Vick for pointing out these papers).

The view “for every learner there exists a distribution in which it fails” is very useful. However I had recently been thinking that is particularly instructive to think of No Free Lunch as a kind of diagnolization argument (this is just a different way of thinking about the prior statement). I am not completely sure if this works but it sounds plausible and makes me see NFL in a different light. It might also be that there is some subtle absrudity or flaw in this kind of thinking. However, I think the NFL theorem can be seen as a simple corollary of the following incompleteness theorem in Kolmogorov Complexity.

Theorem (Chaitin): There exists a constant L (which only depends on the particular axiomatic system and the choice of description language) such that there does not exist a string s for which the statement the “The Kolmogorov Complexity of s is greater than L” (as formalized in S) can be proven within the axiomatic system S. 

Stated informally: “There’s a number L such that we can’t prove the Kolmogorov complexity of any specific string of bits is more than L”. In particular, you can think of any learning machine as a compression scheme (since compression implies learning, we can think of any learning algorithm as a way to compress the data) of some fixed Kolmogorov Complexity (consider the most optimal program for that machine, the programming language is irrelevant as long as it is Turing Complete. Consider the description length of it in bits. That is its Kolmogorov Complexity). Now for any such learning machine (or class of learning machines w.l.o.g) you can construct a data string which has Kolmogorov Complexity greater than what this learning machine has. i.e. this data string is random from the point of view of this learning machine as it is incompressible for it. In short IF the data string has some Kolmogorov Complexity K and your learning machine has Kolmogorov Complexity k and k < K then you will never be able to find any structure in your data string i.e. can never show that it has a KC greater than k. Thus the data string given to our learner would appear to be structureless. Thus no free lunch is just a simple diagonalization argument in the spirit of incompleteness results. One can always construct a string that is Kolmogorov Random or structureless w.r.t our encoding scheme. Ofcourse the Kolmogorov Complexity is uncomputable. However I think the above argument works even when one is talking of upper bounds on the actual Kolmogorov Complexity, but I am not very sure about it or if there are any problems with it.

Also, if one assumes that that there is no reason to believe that structureless functions exist (if we assume that the data is generated by a computational process then there is probably no reason to believe that it is structureless i.e. the problem is “interesting”). And if this is the case, then you would always have a machine in your library of learning algorithms that will be able to find some upper bound on the Kolmogorov Complexity of the data string (much less than the machine itself). This search might be done using Levin’s universal search, for example. I think this line of reasoning leads naturally, to thinking why NFL doesn’t say anything about whether universal learning algorithms can exist.

PS: This thought train about NFL as diagonalization was inspired by a post by David McAllester on what he calls the “Free Lunch Theorem” over here. Some of this appeared as a comment there. However, now I have been inspired enough to study some of the papers concerned including his. (Unrelated to all this. I particularly found likening Chomsky’s Universal Grammar as simply an invocation of NFL on information theoretic grounds in his post very enlightening).

Read Full Post »

The Origin of Kolmogorov Complexity

A mildly personal post.

The title does not imply that the lines quoted below correspond to the exact origin of Kolmogorov Complexity, though they are related and give away the essence.

Andrey Kolmogorov

Information theory must precede probability theory and not be based on it. By the very essence of this discipline, the foundations of information theory have a finite combinatorial character.

– Andrey Kolmogorov

With my background in Electrical Engineering I had the opportunity to take courses in Information Theory and Coding which made the idea of Shannon’s Information Theory quite familiar. But there was a time when I had enough background to started noticing conversations that were perhaps relegated to the background before. Simply because I didn’t know enough to make any sense of them and hence these conversations were more or less noise to me. But these happened to be on Kolmogorov Complexity. I hadn’t sat down and studied it. But had been reading articles here and there that mentioned it even with ideas such as The Godel Incompleteness theorems and the Halting Problem. It created the impression that this area must be fundamental but not clearly why.

And then I came across the above rather cryptic lines by Kolmogorov. Used to the idea of entropy (defined in terms of probability) as information, they made my brain hurt. I spent a couple of days thinking about them and suddenly I realized WHY it was so fundamental. And things started making more sense. Ofcourse I didn’t know anything about it as such, but the two day thinking session convinced me enough, that in a sense it was as fundamental as calculus for me given the things I was interested in (along with Shannon‘s and Fisher’s ideas). It also convinced me enough to want to know more about it no matter what projects I was involved in and immediately bought a book that I have been trying my way through as an aside to what I have been working on (linked below).

I find such insightful one liners that happen to cause almost a phase transition or a complete change in the way you look at some thing (information theory in this case) quite remarkable, making the new view very beautiful. Ofcourse there is a “right” time for them to occur but this was certainly one of them. The lines below had an auxiliary effect too:

The applications of probability theory can be put on a uniform basis. It is always a matter of consequences of hypotheses about the impossibility of reducing in one way or another the complexity of the descriptions of the objects in question. Naturally this approach to the matter does not prevent the development of probability theory as a branch of mathematics being a special case of general measure theory.

The concepts of information theory as applied to infinite sequences give rise to very interesting investigations, which, without being indispensable as a basis of probability theory, can acquire a certain value in investigation of the algorithmic side of mathematics as a whole.

– Andrey Kolmogorov (1983)

While the above was a more personal story there are many other famous examples of cryptic one liners changing a view. Here’s a famous one:

A Famous Cryptic Comment:

Robert Fano

I remember reading a story about the great mathematician and electrical engineer Robert Fano. Around the same time the father of Cybernetics, Norbert Wiener was at MIT and was famous at the time for wandering around campus and then talking to anybody about anything that caught his fancy. There are stories on how graduate students would run away when Wiener was sighted coming to save their time. Wiener’s eccentricities are famous (recommendation [2] below) but let me not digress. In one of his routine days he appeared in the office of Fano and made a cryptic comment:

You know, information is entropy.

Fano spent a good time thinking about what this might mean and he has himself remarked that it was in part responsible for his developing, completely independently the first law of Shannon’s theory. Claude Shannon even cited Fano in his famous paper.

I can’t help thinking that such one liners are perhaps the best examples of information compression and Kolmogorov complexity.

_________________________

Recommendations:

1. An Introduction to Kolmogorov Complexity and its Applications – Ming Li and Paul Vitanyi (on the basis of the first third)

2. Dark Hero of the Information Age – Conway and Siegelman

_________________________

Earlier Related Post:

1. Ray Solomonoff is No More (has a short discussion on Solomonoff’s ideas in the same. It is noteworthy that Solomonoff published the first paper in what is today called Kolmogorov Complexity. His approach to the area was through Induction.  Kolmogorov and Chaitin approached it from randomness).

Read Full Post »

In Praise of Leibniz

There are two kinds of truths: those of reasoning and those of fact. The truths of reasoning are necessary and their opposite is impossible; the truths of fact are contingent and their opposites are possible. (The Monadology of Leibniz)

The past few months have made me realize more and more about the sheer number of fundamental ideas that can be traced back, atleast in part to Gottfried Leibniz. The ones that I find most striking (other than his countless other contributions in calculus, geology, physics, philosophy, rationality, theology etc.) given what has been on my mind recently are his ideas in formal systems, symbolic logic and Kolmogorov Complexity.

It is not incorrect to think that Leibniz could be considered the first computer scientist to have lived. His philosophy centered around having a universal language of symbols combined with a calculus of reasoning, something from which modern symbolic logic and notation has directly descended from. An interest in mathematical logic also directly leads to an interest in the “mechanization of thought”, the same could be seen in Leibniz who was a prolific inventor of calculating devices.

His elucidation of what might be called the earliest ideas in Algorithmic Information Theory/Kolmogorov Complexity is equally intriguing. While he explicates them in depth, what he essentially talks about is the complexity of an “explanation” (basically Kolmogorov Complexity). And that an arbitrarily complex explanation is no explanation at all. I also find this idea similar to the bias-variance tradeoff in machine learning and the problem of overfitting. What I find striking is the clarity with which these ideas had been expressed and how little they have changed in essence in 3 centuries (though formalized).

In my intrigue, I have tried to read his very short works – Discours de métaphysique and The Monadology. While these have been debated over the centuries, their fundamental nature is unquestioned and are a recommended read. More recently I mentioned that I had been really intrigued by Leibniz for some months to my teacher from the undergraduate days. He was instrumental in getting me to read Cybernetics (by Norbert Wiener) and in Signal Processing in general. He was quick to point to this paragraph from Wiener’s book that I did not even remember reading:

Norbert Wiener

Since Leibniz there has perhaps been no man who has had a full command of all the intellectual activity of his day. Since that time, science has been increasingly the task of specialists, in fields which show a tendency to grow progressively narrower. A century ago there may have been no Leibniz, but there was a Gauss, a Faraday, and a Darwin. Today there are few scholars who can call themselves mathematicians or physicists or biologists without restriction.

A man may be a topologist or an acoustician or a coleopterist. He will be filled with the jargon of his field, and will know all its literature and all its ramifications, but, more frequently than not, he will regard the next subject as something belonging to his colleague three doors down the corridor, and will consider any interest in it on his own part as an unwarrantable breach of privacy.

– Norbert Wiener, Cybernetics or the Control and Communication in the Animal and the Machine. 1948.

Since the mention of Wiener has occurred, it might also be useful to consider his trenchant advice just before the start of the above passage:

For many years Dr. Rosenblueth and I had shared the conviction that the most fruitful areas for the growth of sciences were those which had been neglected as a no-man’s land between the various established fields […]

_________________________

Onionesque Reality Home >>

Read Full Post »

Ray Solomonoff is No More

For the past couple of years, I have had a couple of questions about machine learning research that I have wanted to ask some experts, but never got the chance to do so. I did not even know if my questions made sense at all. I would probably write about them on a blog post soon enough.

It is however ironical that I came to know my questions were valid and well discussed (I never knew what to search for them, I used expressions not used by researchers) only by the death of Ray Solomonoff (he was one researcher who worked on it, and an obituary on him highlighted his work on it, something I missed). Solomonoff was one of the founding fathers of Artificial Intelligence as a field and Machine Learning as a discipline within it. It must be noted that he was one of the few attendees at the 1956 Dartmouth Conference, basically an extended brain storming session that started AI formally as a field. The other attendees were : Marvin Minsky, John McCarthy, Allen Newell, Herbert Simon, Arthur Samuel,  Oliver Selfridge, Claude Shannon, Nathaniel Rochester and Trenchand Moore. His 1950-52 papers on networks are regarded as the first statistical analysis of the same.  Solomonoff was thus a towering figure in AI and Machine Learning.

[Ray Solomonoff  : (25 July 1926- 7 December 2009)]

Solomonoff is widely considered as the father of Machine Learning for circulating the first report on the same in 1956. His particular focus was on the use of probability and its relation to learning. He founded the idea of Algorithmic Probability (ALP)  in a 1960 paper at Caltech, an idea that gives rise to Kolmogorov Complexity as a side product. A. N. Kolmogorov independently discovered similar results and came to know of and acknowledged Solomonoff’s earlier work on Algorithmic Information Theory. His work however was relatively unknown in the west than in the soviet union, which is why Algorithmic Information Theory is mostly referred to as Kolmogorov complexity rather than “Solomonoff Complexity”. Kolmogorov and Solomonoff approached the same framework from different directions. While Kolmogorov was concerned with randomness and Information Theory, Solomonoff was concerned with inductive reasoning. And in doing so he discovered ALP and Kolomogorov Complexity years before anyone did. I would write below on only one aspect of his work that I have studied to some degree in the past year.

Solomonoff With G.J Chaitin, another pioneer in Algorithmic Information Theory

[Image Source]

The Universal Distribution:

His 1956 paper, “An inductive inference machine” was one of the seminal papers that used probability in Machine Learning. He outlined two main problems which he thought (correctly) were linked.

The Problem of Learning in Humans : How do you use all the information that you gather in life in making decisions?

The Problem of Probability : Given you have some data and some a-priori information, how can you make the best possible predictions for the future?

The problem of learning is more general and related to the problem of probability. Solomonoff noted that the Machine learning was simply the process of approximating ideal probabilistic predictions for practical use.

Building on his 1956 paper, he discovered probabilistic languages for induction at a time when it was considered out of fashion. And discovered the Universal Distribution.

All induction problems could be basically reduced to this form : Given a sequence of binary symbols how do you extrapolate it? The answer being that we could assign a probability to a sequence and then use Bayes Theorem to make a prediction on which particular continuation of a string was how likely. That gives rise to an even more difficult question that was the basic question for a lot of Solomonoff’s work and on Algorithmic Probability/Algorithmic Information Theory. This question is : How do you assign probabilities to strings?

Solomonoff approached this problem using the idea of a Universal Turing Machine. Suppose this Turing Machine has three types of tapes, an unidirectional input tape, an unidirectional output tape and a bidirectional working tape. Suppose this machine will take some binary string as input and it may give a binary string as output.

It could do any of the following :

1. Print out a string after a while and then come to a stop.

2. It could print an infinite output string.

3. It could go in an infinite loop for computing the string and not output anything at all (Halting Problem).

For a string , the ALP would be as follows :

If we feed some bits at random to our Turing Machine, there will always be some probability that the output would start with a string . This probability is the algorithmic or universal probability of the string .

The ALP would be given as :

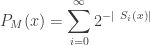
Where 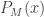would be the universal probability of string with respect to the universal turing machine 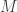. To understand the placement of 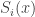in the above expression, let’s discuss it a little.

There could be many random strings that after being processed by the Turing Machine give an output string that begins with string . And 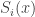is the 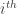such string. Each such string carries a description of . And since we want to consider all cases, we take the summation. In the expression above 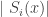gives the length of a string and the probability that the random input 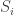would output a string starting with .

This definition of ALP has the following properties that have been stated and proved by Solomonoff in the 60s and the 70s.

1. It assigns higher probabilities to strings with shorter descriptions. This is the reverse of something like Huffman Coding.

2. The value for ALP would be independent of the type of the universal machine used.

3. ALP is incomputible. This is the case because of the halting problem. Infact it is this reason that it has not received much attention. Why get interested in a model that is incomputible? However Solomonoff insisted that approximations to the ALP would be much better than existing systems and that getting the exact ALP is not even needed.

4. 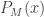is a complete description for . That means any pattern in the data could be found by using . This means that the universal distribution is the only inductive principle that is complete. And approximations to it would be much desirable.

__________

Solomonoff also worked on Grammar discovery and was very interested in Koza’s Genetic Programming system, which he believed could lead to efficient and much better machine learning methods. He published papers till the ripe old age of 83 and is definitely inspiring for the love of his work.  Paul Vitanyi notes that :

It is unusual to find a productive major scientist that is not regularly employed at all. But from all the elder people (not only scientists) I know, Ray Solomonoff was the happiest, the most inquisitive, and the most satisfied. He continued publishing papers right up to his death at 83.

Solomonoff’s ideas are still not exploited to their full potential and in my opinion would be necessary to explore to build the Machine Learning dream of never-ending learners and incremental + synergistic Machine Learning. I would write about this in a later post pretty soon. It was a life of great distinction and a life well lived. I also wish strength and peace to his wife Grace and his nephew Alex.

The five surviving (in 2006) founders of AI who met in 2006 to commemorate 50 years of the Dartmouth Conference. From left : Trenchand Moore, John McCarthy, Marvin Minsky, Oliver Selfridge and Ray Solomonoff

__________

Refernces and Links:

1. Ray Solomonoff’s publications.

2. Obituary: Ray Solomonoff – The founding father of Algorithmic Information Theory by Paul Vitanyi

3. The Universal Distribution and Machine Learning (PDF).

4. Universal Artificial Intelligence by Marcus Hutter (videolectures.net)

5. Minimum Description Length by Peter Grünwald (videolecures.net)

6. Universal Learning Algorithms and Optimal Search (Neural Information Processing Systems 2002 workshop)

__________

Onionesque Reality Home >>

Read Full Post »